- 时间点：
- 时 分 秒 当前视频时间点
- 问题：
-
- 选项一
设为正确答案
新增选项 - 选项一
- 正确跳转时间：
- 时 分 秒 同锚点时间
- 错误跳转时间：
- 时 分 秒 同锚点时间
恭喜你，回答正确~
很遗憾，回答错误~
正确答案： ,您可以
从年龄特点来看，初三的学生好动、好奇、好表现，抓住学生特点，积极采用形象生动、形式多样的方法和学生广泛、积极、主动参与的活动，定能激发学生兴趣，有效的培养学生能力。心理上，青少年注意力易分散，爱发表见解，希望得到老师的表扬，所以在教学中应抓住学生这一心理特点，一方面要运用直观生动的形象，引发学生的兴趣，使他们的注意力始终集中在课堂上；另一方面要创造条件和机会，让学生发表见解，发挥学生学习的相象力和创造力。
多媒体课件，预习学案，数学实验报告，铅笔，直尺，计算器等
知识技能：
（1）使学生理解锐角正弦的定义。
（2）会求直三角形中锐角的正弦值。
（3）熟记特殊角30°，45°，60°角的正弦值，并能根据这些值说出对应的锐角度数。
数学思考
通过探索正弦定义，培养学生观察、比较、分析、概括等逻辑思维能力。
问题解决
通过合作交流，能够根据直角三角形中边角关系，进行简单的计算。
情感态度
（1）在自主探索、共同发现、共同交流的过程中分享成功的喜悦；
（2）在讨论的过程中使学生感受集体的力量，培养团队意识；
（3）通过探索
、发现、培养学生独立思考，勇于创新的精神和良好的学习习惯。
重点：
1、理解和掌握锐角正弦的定义。
2、根据定义求锐角的正弦值。
难点：
探索“在直角三角形中，任意锐角的对边与斜边的比值是一个常数”的过程。
坚持“以学生活动为主，教师讲述为辅，学生活动在前，教师点拨评价在后”的原则，根据学生的规律，理论联系实际安排教学内容，采用学生参与程度高的导学教练评的方式，学习基础性知识和技能，培养动机，明确学习目的。教师在课堂上充分调动学生的学习积极性，激发来自学生主体的最有力的动力。
导入明标
1、如图，在Rt⊿ABC中，∠C=90°;∠A的对边是 ，∠A的邻边是 ，斜边是 。
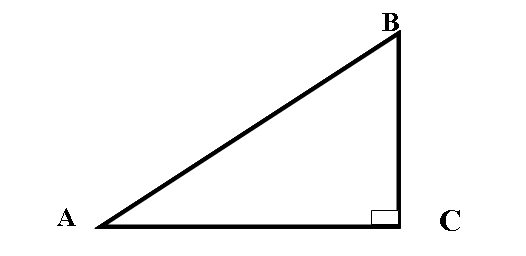
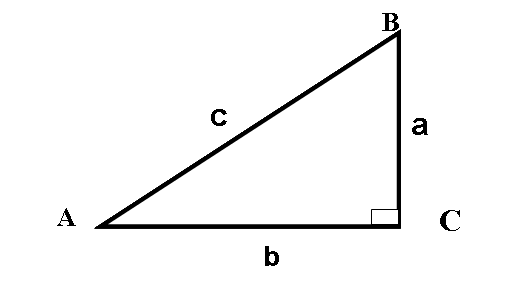
2、如图，在Rt⊿ABC中，∠C=90°，三边之间满足的关系式： ；
3、在直角三角形中，30°的角所对的直角边与斜边之间的关系： ，
用字母表示 。
探究交流
动手操作：
1.画一个直角三角形，其中一个锐角为60°； 2.量出60°角的对边、邻边和斜边长度； 3.计算 60°角对边与斜边的比；
探究交流：小组进行交流、讨论。
1、计算出对应的比值是否相等（精确到0.01）？
2、你们画出的直角三角形相似吗？能证明你的结论吗？ ��
3、你是如何理解正弦的？
教师精讲
1、小组讨论得到的结论：
2、问题转化：
已知：任意两个直角三角形△ABC和△A’B’C’， ∠C =∠C’= 90º ，∠A =∠A ' ，
求证：
类似地可以证明：在有一个锐角等于α的所有直角三角形中，角α的对边与斜边的比值为一个常数．
定义： 在直角三角形中，锐角α的对边与斜边的比叫做角α的正弦，记作: 
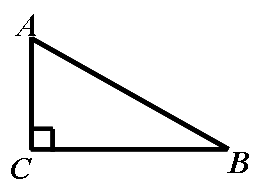
练习：如图，在直角三角形ABC中， ∠C= 90º，
求：(1)、表示sinA; (2)、表示sinB;
例：如图，在直角三角形ABC中， ∠C= 90º， BC=3，AB=5．(1)、求sinA; (2)、求sinB. 
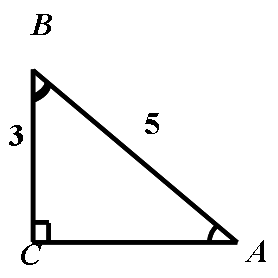
练习：在Rt △ABC 中， ∠C= 90º， AC=5，AB=7． 求sinA 的值．
如何求sin 45°的值？
如图所示，构造一个Rt△ABC，使∠C=90°，∠A=45°.于是 ∠B=45°从而AC=BC．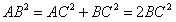
于是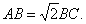 
如何求sin 60°的值？
如图所示，构造一个Rt△ABC ，使∠B=60°，则∠A=30°，从而 BC=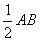
，
根据勾股定理,得
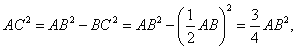
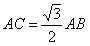所以
，所以
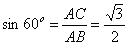
学习展示
1、一艘帆船从西向东航行到 C处时，灯塔A在船的正北方向， 帆船从C处继续向正东方向航行2000米到达B处，此时灯塔A在船的北偏西60º的方向． 问：B处和灯塔A的距离约等于多少米？（精确到1m）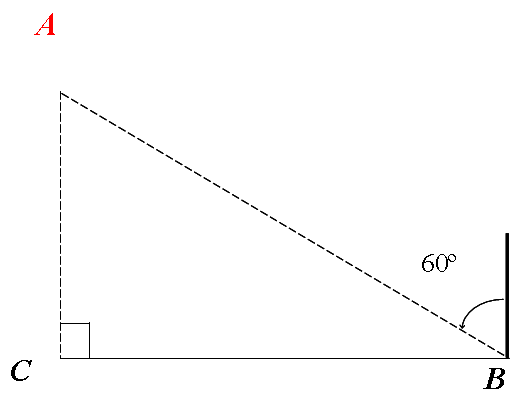
抽象出数学问题： 已知在RtΔABC中 ，∠C=90°，∠A=60°， BC=2000米，求：AB的长度。（精确到1m）（其中Sin60°≈0.87）
2、在Rt⊿ABC中，∠C=900，AB=20，sinB=0.8，求AC和BC的长。
3、在等腰△ABC中，AB=AC=5，BC=6， 求sinB.
课堂小结
同学们，通过本节课的学习，把你对知识的理解，以及自己的收获和同学们共同分享一下吧！
当堂检测
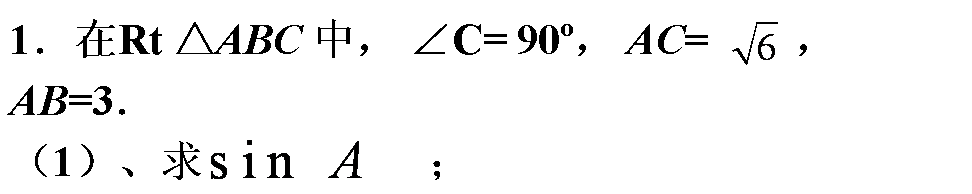
设为正确答案
